IFS生成分形图案

最近看到一种分形图案hexaflake，其介绍可以在wiki看到，尝试使用python来生成这个图案。

IFS

生成方法叫做IFS，迭代函数系统。IFS方法通过迭代的方式生成一系列的点(x, y)，最后把这些点画出来即可。每次迭代是通过叫做IFS码表的东西，从$(x_k, y_k)$得到$(x_{k+1}, x_{k+1})$：

$$
\left[
\begin{matrix}
x_{k+1}\\
y_{k+1}\\
\end{matrix}
\right] =
\left[
\begin{matrix}
a&b\\
c&d\\
\end{matrix}
\right]
\left[
\begin{matrix}
x_{k}\\
y_{k}\\
\end{matrix}
\right]
+
\left[
\begin{matrix}
e\\
f\\
\end{matrix}
\right]
$$

其中a, b, c, d组成的矩阵作用是压缩，旋转，e, f是平移。
一些最简单的分形图案，基本上其整体和局部的关系就是压缩之后再平移。将a, b, c, d矩阵改写成如下形式，可以得到其明确的意义。
$$
\left[
\begin{matrix}
a&b\\
c&d\\
\end{matrix}
\right] =
\left[
\begin{matrix}
rcos\theta&-ssin\phi\\
rsin\theta&scos\phi\\
\end{matrix}
\right]
$$
其中$r, s$分别是x和y轴的缩放系数，$\theta$，$\phi$是x，y轴旋转的角度。

Sierpinski

Sierpinski分形是一种简单的分形，用一个简单的Sierpinski分形来介绍IFS码表怎么获得。

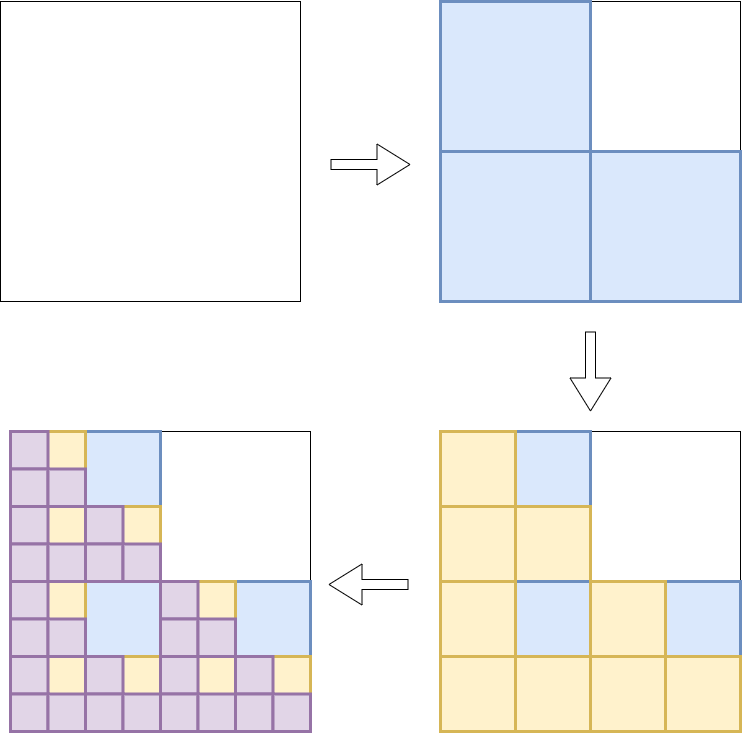
示意图中可以看出，每一步都做了如下操作：

1. 把整体大正方形沿x, y方向缩小1/2，然后放在三个位置
2. 位置一：无平移
3. 位置二：y方向平移1/2
4. 位置三：x方向平移1/2
   IFS表用来表示三个位置用到的是概率，在一次迭代中，平移到三个位置的概率是一样的，都是1/3。那么IFS码表是

最后生成的图形是

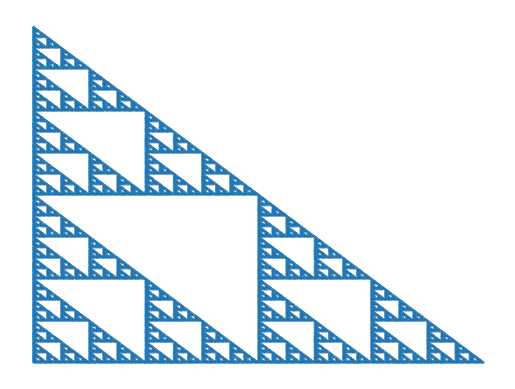
hexaflake

同样的，根据hexaflake的图形，可以总结其迭代中的变换。

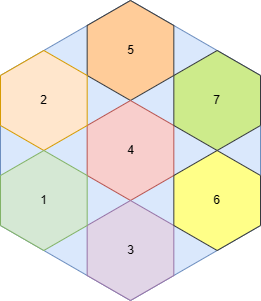
设原正六边形正对的顶点到顶点的长度l_pp是1，那么，边长是1/2，正对的边到边距离l_ee是cos(pi/6)。
首先可以看出一个大的正六边形，迭代是分成七个小正六边形，缩小的比例是1/3，无旋转。

编号1位置，向上平移了一个小六边形的边长，可以计算出边长是1/6。f=1/6。
编号2位置，向上平移了三个小六边形的边长
编号3位置，右移1/3个l_ee
编号4位置，右移1/3个l_ee，上移1/3
…

据此可以得到IFS码表

其python代码实现是：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import matplotlib.pyplot as plt
import numpy as np
import random
from math import cos, sin, pi

n = 500000
x = np.zeros(n)
y = np.zeros(n)

v = 1/6
h = cos(pi/6)/3
x[0] = 0.5

for k in range(1,n):
    p = random.random()
    if p < 1/7:
        x[k] = 1/3 * x[k-1] + 0 * y[k-1]
        y[k] = 0 * x[k-1] + 1/3 * y[k-1] + v
    elif p < 2/7:
        x[k] = 1/3 * x[k-1] + 0 * y[k-1]
        y[k] = 0 * x[k-1] + 1/3 * y[k-1] + 3*v
    elif p < 3/7:
        x[k] = 1/3 * x[k-1] + 0 * y[k-1] + h
        y[k] = 0 * x[k-1] + 1/3 * y[k-1]
    elif p < 4/7:
        x[k] = 1/3 * x[k-1] + 0 * y[k-1] + h
        y[k] = 0 * x[k-1] + 1/3 * y[k-1] + 1/3
    elif p < 5/7:
        x[k] = 1/3 * x[k-1] + 0 * y[k-1] + h
        y[k] = 0 * x[k-1] + 1/3 * y[k-1] + 2/3
    elif p < 6/7:
        x[k] = 1/3 * x[k-1] + 0 * y[k-1] + 2*h
        y[k] = 0 * x[k-1] + 1/3 * y[k-1] + v
    else:
        x[k] = 1/3 * x[k-1] + 0 * y[k-1] + 2*h
        y[k] = 0 * x[k-1] + 1/3 * y[k-1] + 3*v

plt.scatter(x,y,s=0.0003)
plt.axis('off')
plt.show()

生成的图形是

图案中还到处可以看到koch雪花。

参考

基于迭代函数系统的分形植物模拟